Artem Krylysov

Why another key-value store? #

I needed a store that could map keys to values with the following requirements:

• The number of keys was large and I couldn't keep the items in memory (that would require switching to more expensive server instance type).

• Low latency. I wanted to avoid network overhead if it was possible.

• I needed to rebuild the mapping once a day and then access it in read-only mode.

• The sequential lookup performance wasn't important, all I cared about was random lookup performance.

There are plenty of open-source key-value stores - the most popular are LevelDB, RocksDB and LMDB. Also there are some key-value stores implemented in Go - e.g. Bolt, goleveldb (port of LevelDB) and BadgerDB.

I tried to use LevelDB and RocksDB in production, but unfortunately, the observed results didn't meet the performance requirements.

The stores I mentioned above are not optimized for a specific use case - they are general-purpose solutions. For example, LevelDB supports range queries - allows iterating over keys in lexicographic order, supports caching, bloom filters and many other nice features, but I didn't need any of those features. The common implementation of key-value stores is based on tree algorithms. Usually it's B+ trees or LSM trees. Both data structures always require several I/O operations per lookup.

A hash table with a constant average lookup time seemed like a better choice. At least in theory a hash table beats a tree for my use case, so I decided to implement a simple on-disk hash table and benchmark it against LevelDB.

File layout #

Pogreb uses two files to store keys and values.

+----------+
| header   |
+----------+
| bucket 0 |
| ...      |
| bucket N |
+----------+

+------------------------+
| slot 0                 |
| ...                    |
| slot N                 |
+------------------------+
| overflow bucket offset |
+------------------------+

+------------------+
| key hash         |
+------------------+
| key size         |
+------------------+
| value size       |
+------------------+
| key/value offset |
+------------------+

Algorithm #

Pogreb uses the Linear hashing algorithm which grows the index file one bucket at a time instead of rebuilding the whole hash table.

Initially, the hash table contains a single bucket (N=1).

Level L (initially L=0) represents the maximum number of buckets on a logarithmic scale the hash table can have. For example, a hash table with L=0 contains between 0 and 1 buckets; L=3 contains between 4 and 8 buckets.

S is the index of the "split" bucket (initially S=0).

Collisions are resolved using bucket chaining method. Overflow buckets are stored in the data file and form a linked list.

           Index file
          +----------+
          | bucket 0 |                 Bucket
          | ...      |    +------------------------------+
h(key) -> | bucket X | -> | slot 0 ... slot Y ... slot N |
          | ...      |    +------------------------------+
          | bucket N |                    |
          +----------+                    |
                                          |
                                          v
                                      Data file
                                    +-----------+
                                    | key-value |
                                    +-----------+

Memory-mapped file #

Both index and data files are stored entirely on disk. The files are mapped into the process's virtual memory space using the mmap syscall on Unix-like operating systems or using the CreateFileMapping WinAPI function on Windows.

Switching from a regular file I/O to mmap for lookup operations gave nearly 100% performance boost.

Durability #

Pogreb makes an important assumption - it assumes that all 512-byte sector disk writes are atomic. Each bucket is precisely 512 bytes and all allocations in the data file are 512-byte aligned. The insertion operation doesn't overwrite the old data in the data file - it writes a new key/value pair first, then updates the bucket in-place in the index file. If both operations are successful, the space allocated by the old key/value is added to the free list.

Pogreb doesn't flush changes to disk (fsync operation) automatically. Data that is not flushed may be lost in case of power loss. However, application crash shouldn't cause any issues. There is an option to make Pogreb fsync changes to disk after each write - set BackgroundSyncInterval to -1. Alternatively DB.Sync can be used at any time to force the OS to write the data to disk.

Concurrency #

Pogreb supports multiple concurrent readers and a single writer - write operations are guarded with a mutex.

API #

The API is similar to the LevelDB API - it provides methods like Put, Get, Has, Delete and supports iteration over the key/value pairs (the Items method):

package main

import (
    "log"

    "github.com/akrylysov/pogreb"
)

func main() {
    // Opening a database.
    db, err := pogreb.Open("example", nil)
    if err != nil {
        log.Fatal(err)
        return
    }
    defer db.Close()

    // Writing to a database.
    err = db.Put([]byte("foo"), []byte("bar"))
    if err != nil {
        log.Fatal(err)
        return
    }

    // Reading from a database.
    val, err := db.Get([]byte("foo"))
    if err != nil {
        log.Fatal(err)
        return
    }
    log.Printf("%s", val)

    // Iterating over key/value pairs.
    it := db.Items()
    for {
        key, val, err := it.Next()
        if err == pogreb.ErrIterationDone {
            break
        }
        if err != nil {
            log.Fatal(err)
        }
        log.Printf("%s %s", key, val)
    }
}

Unlike LevelDB's iterator, Pogreb's iterator returns key/value pairs in an unspecified order - you get constant time lookups in exchange for losing range and prefix scans.

All API methods are safe for concurrent use by multiple goroutines.

Performance #

I created a tool to benchmark Pogreb, Bolt, goleveldb and BadgerDB. The tool generates a given number of random keys (16-64 byte length) and writes random values (128-512 byte length) for the generated keys. After successfully writing the items, pogreb-bench reopens the database, shuffles the keys and reads them back.

The benchmarks were performed on a DigitalOcean droplet with 8 CPUs / 16 GB RAM / 160 GB SSD + Ubuntu 16.04.3:

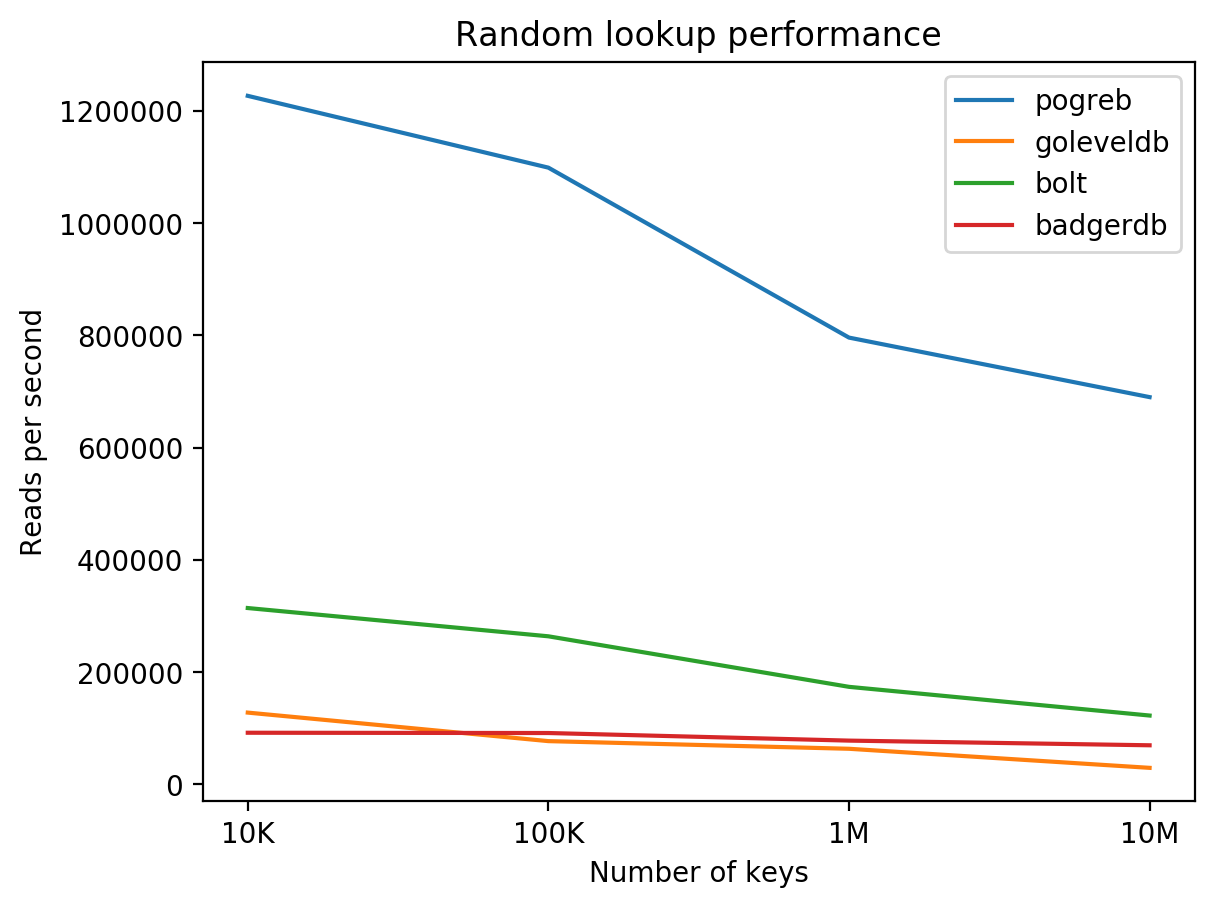
Conclusion #

Choosing the right data structure and optimizing the store for the specific use case (random lookups) allowed to make Pogreb significantly faster than similar solutions.

Pogreb on Github - https://github.com/akrylysov/pogreb.